In times of Big Data, the graph has become a popular data structure due to its flexible and clear relationship-based structure. Even entire database systems are now designed according to the graph principle. For more on this, read our article on NoSQL databases. Libraries, like PyGraph, allow you to perform fast queries and optimized graph manipulations. With its full Python implementation, it offers you a user-friendly and powerful tool.
What is a graph?
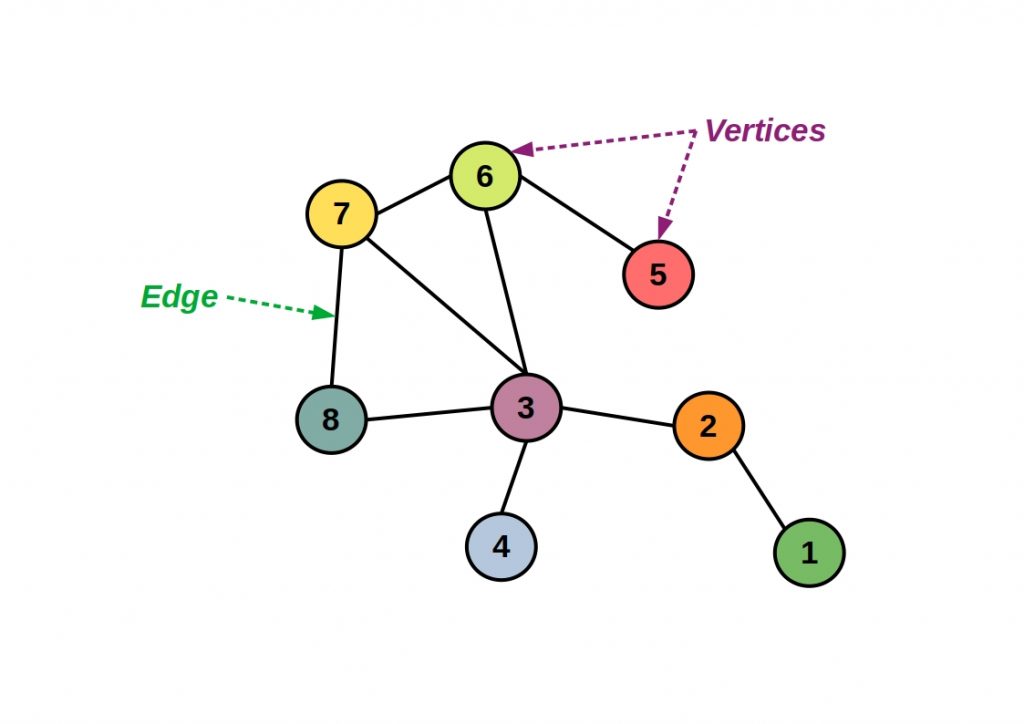
In a graph, objects are represented according to their relationships with each other. The objects are called vertices and the relations are called edges of the graph. An edge always connects exactly two nodes.
Graphs are often used to represent traffic networks, entity-relationship diagrams, syntax trees for programming languages, finite automata and proof or decision trees.


PyGraph supports different graph types
Basically, graphs must be differentiated between directed and undirected.
If a graph is directed, the edges may only be used in one direction. These edges are also called directed edges. If it is undirected, there are no directional constraints. So each edge is connected to an undirected pair of vertices. In the following figure we have contrasted both categories.
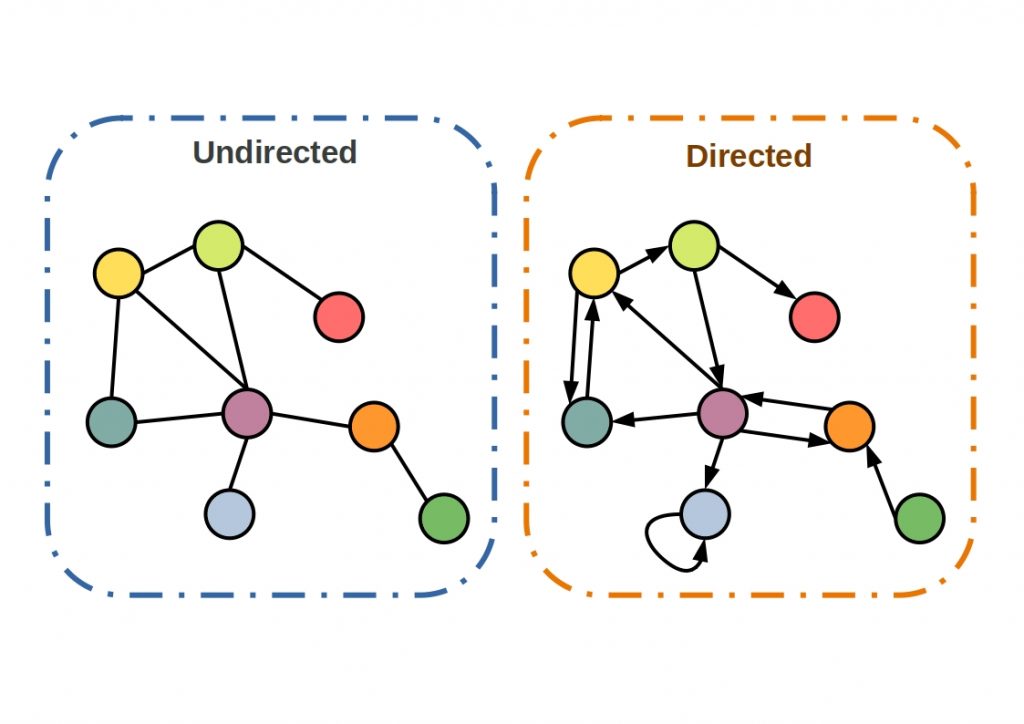


You can use PyGraph regardless of these properties, because both types are supported.
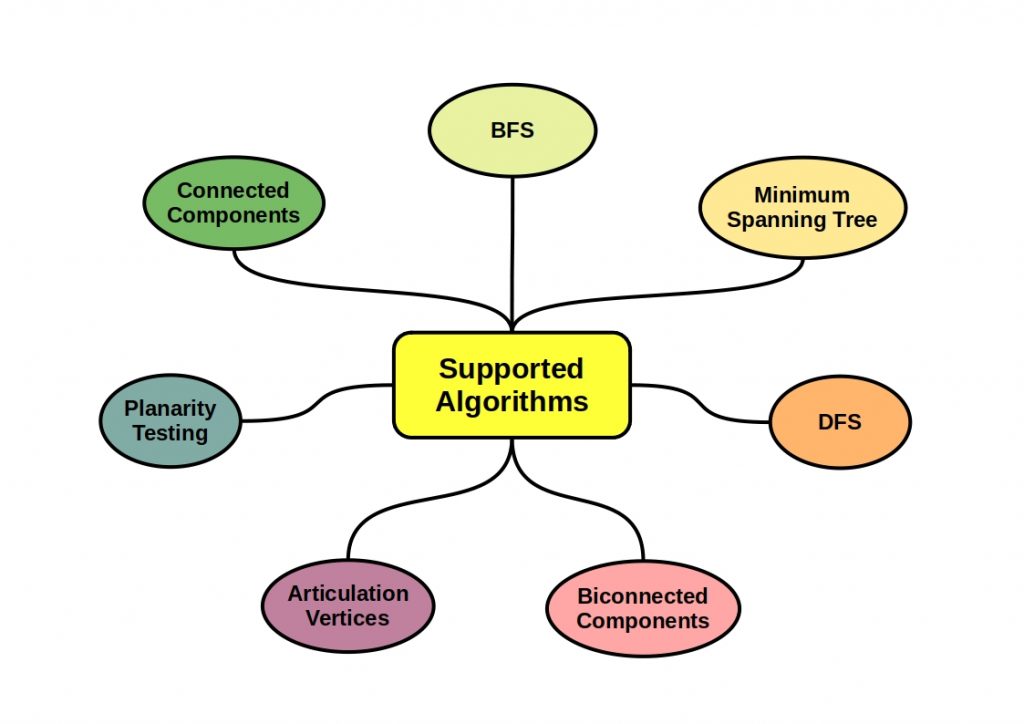
PyGraph supports several algorithms
PyGraph supports the use of many well-known graph operations. For example, searching or traversing a graph, where all nodes of a graph must be visited, can be done in different ways. In the Depth-First Search (DFS) search algorithm, for example, the successors of a successor of the current node are visited first and only then the neighbors of the current node.
The depth of the search can also be limited accordingly. Breadth-First Search (BFS), on the other hand, first visits its own neighboring nodes and only then the successors of the neighboring nodes.
In addition to the algorithm-based search of a graph, other operations can be performed with PyGraph, such as the calculation of minimum spanning trees. This tree describes the best possible path to traverse all available nodes in a weighted graph. In the following figure we have shown you all currently supported algorithms.