The machine learning algorithm t-Distributed Stochastic Neighborhood Embedding, also abbreviated as t-SNE, can be used to visualize high-dimensional datasets. Each high-dimensional information of a
data point is reduced to a low-dimensional representation. However, the information about existing neighborhoods should be preserved.
So this technique is another tool you can use to create meaningful groups in unordered data collections based on the unifying data properties. If you don’t know what cluster algorithms are, check out this article. Here we present 5 machine learning methods that you should know.
As shown in the following figure, the data should be represented grouped in 2-dimensional space.
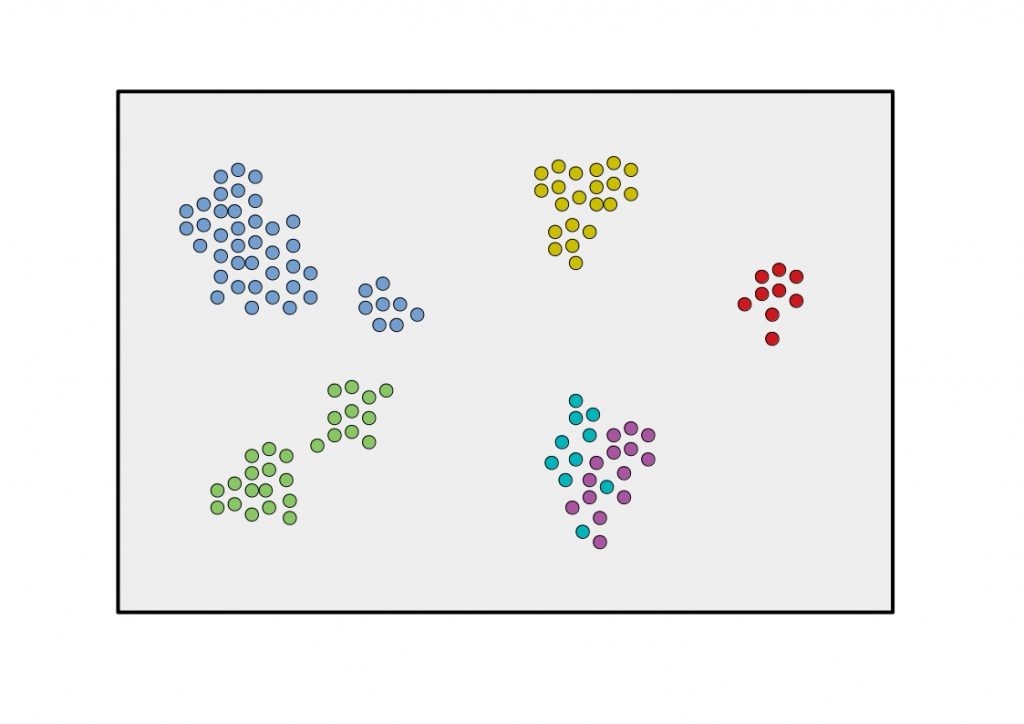


But how does the algorithm work and what are its strengths? In order to understand its function, we need to look at the origin of the technology.
What is the Stochastic Neighbor Embedding (SNE) Algorithm?
The basis of the t-Distributed Stochastic Neighborhood Embedding algorithm is originally the Stochastic Neighbor Embedding (SNE) algorithm. This converts high-dimensional Euclidean distances into similarity probabilities between individual data points.
The probability with which an object occurs next to a potential neighbor must be calculated.
The dissimilarities between two high-dimensional data points can be explained with a distance matrix, corresponding to the squared Euclidean distance.
A conditional probability is calculated for the low-dimensional correspondence.
This determines the similarity of the two data points on the low-dimensional map.
In order to achieve the closest possible correspondence between the two distributions pij and
qij, a Kullback-Leibler divergence (KL) over all neighbors of each data point is computed as a cost function C. Large costs are incurred for distant data points.
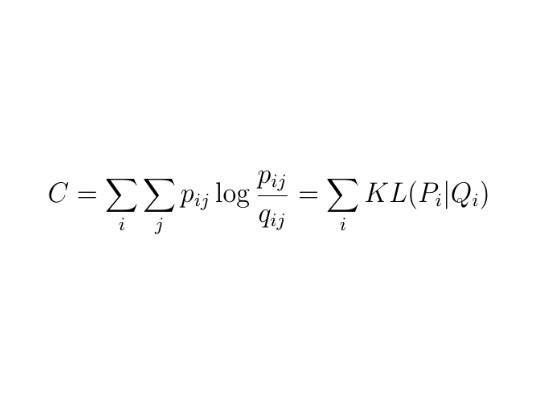
A gradient descent method is used to optimize the cost function. However, this optimization method converges very slowly. In addition, a so-called crowding problem arises.
If a high dimensional data set is linearly approximated in a small scale, then it cannot be reduced to a lower dimension with a local scaling algo-
rithm to a lower dimension.
What makes the t-Distributed Stochastic Neighborhood Embedding (t-SNE) Algorithmt work?
The t-Distributed Stochastic Neighbor
Embedding (t-SNE) algorithm starts here. On the one hand, a simplified symmetric cost function is used.
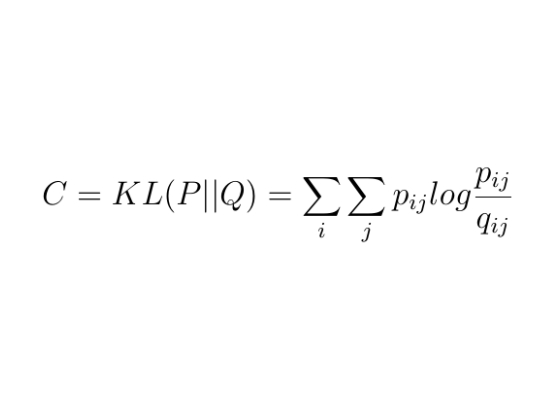
Here, only one KL is minimized over a common probability distribution of all
high, and low dimensional data is minimized.
On the other hand, the similarity of the low-dimensional data points is computed with a Student’s t-distribution and a degree of freedom of one. This can be optimized quickly and is stable to the crowding problem.
stable against the crowding problem.

Leave a Reply