Page 2 of 4

Messaging Patterns – It is not enough to decide to use a message

January 17, 2021 / RainerGewalt / 1 Comment

Messaging Patterns- What are they? What are their strengths and why should they only be used with caution? We clarify these questions in this article.

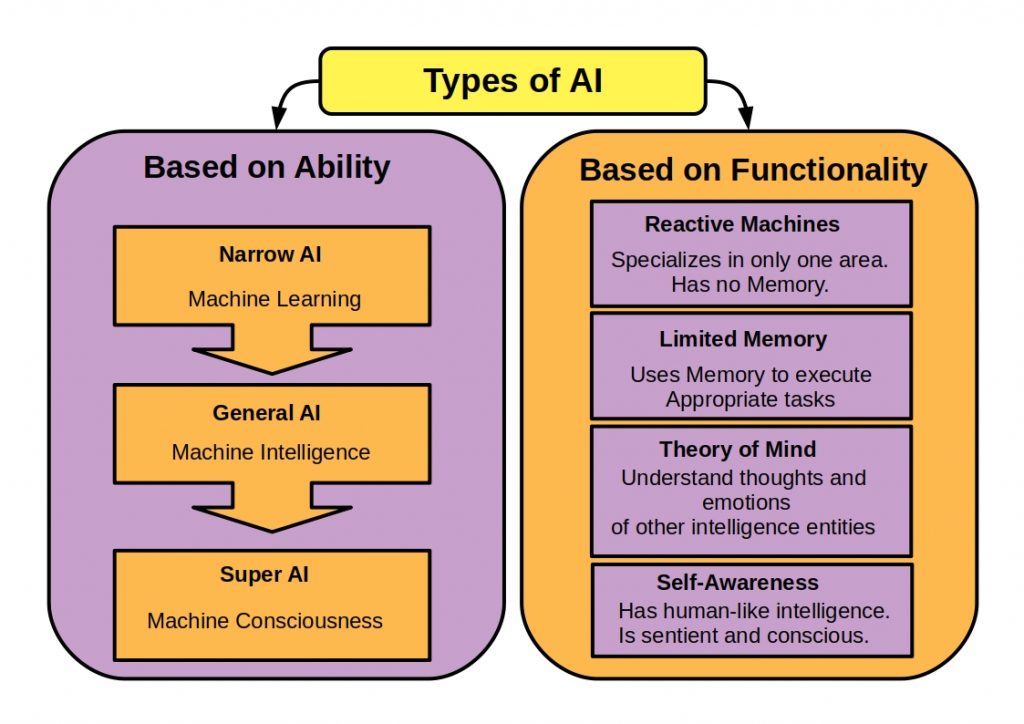
What are Design Patterns?

Technology-independent designs can provide proven pattern solutions in software development, ensuring standardized and robust architecture.
If you’ve never heard of software design patterns, check out this article from us on the subject first.

Design patterns allow a developer to draw on the experience of others. They offer proven solutions for recurring tasks. A one-to-one implementation is not advisable. The patterns should rather be used as a guide.

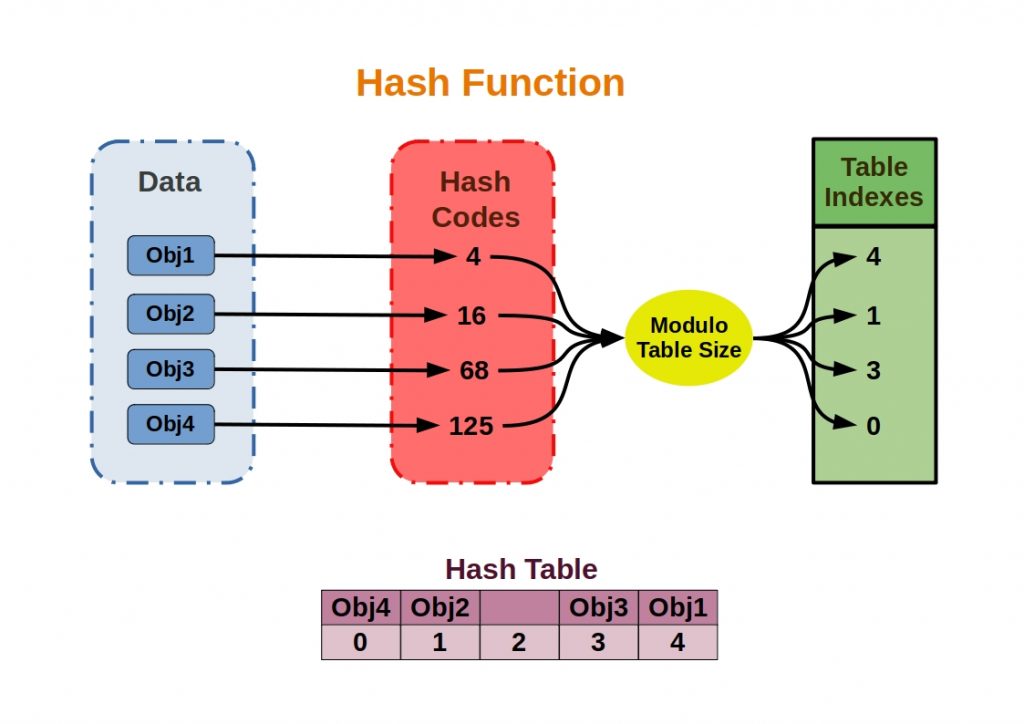
What is a message?

A basic design pattern is the message. Actually a term that is used by everyone as a matter of course, but what is behind it?

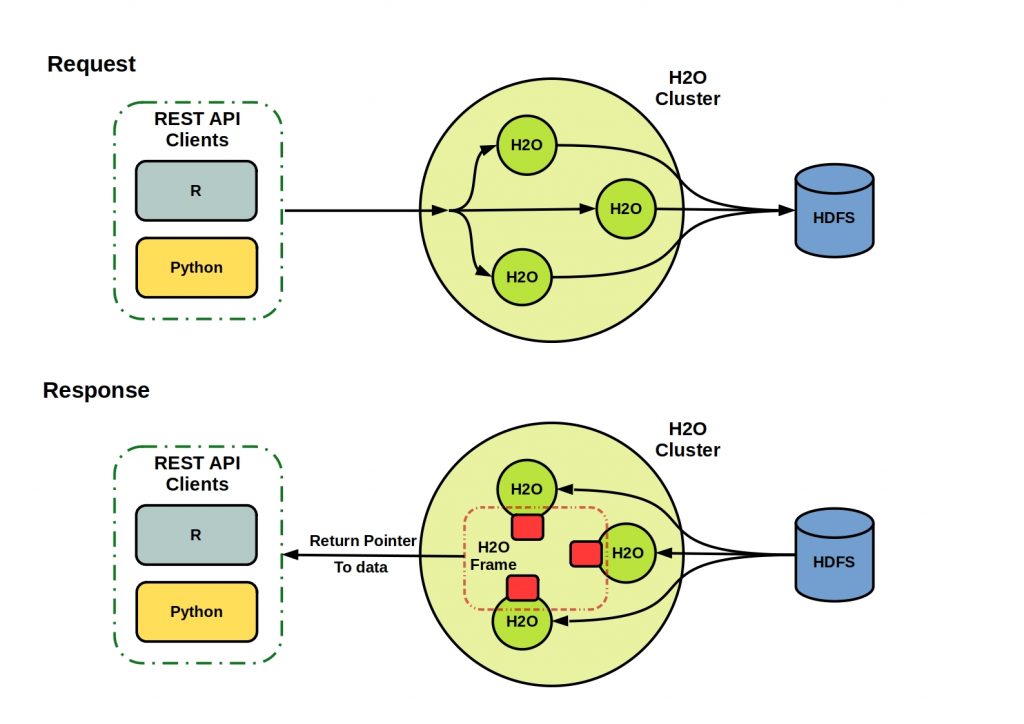
Data is packaged in messages and then transmitted from the sender to the receiver via a message channel. The following figure shows such a messaging system.

Messaging Patterns - This scheme shows the basic concept of a message — Messaging Patterns – Basic Concept of a Message

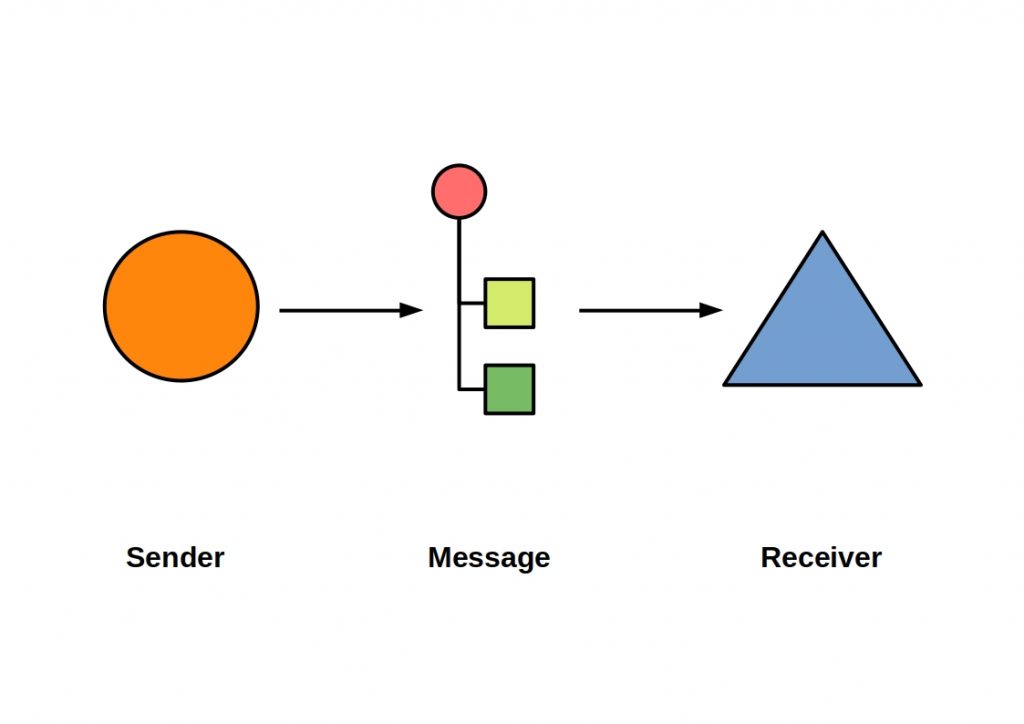
The communication is asynchronous, which means that both applications are decoupled from each other and therefore do not have to run simultaneously. The sender must build and send the message, while the receiver must read and unpack it.

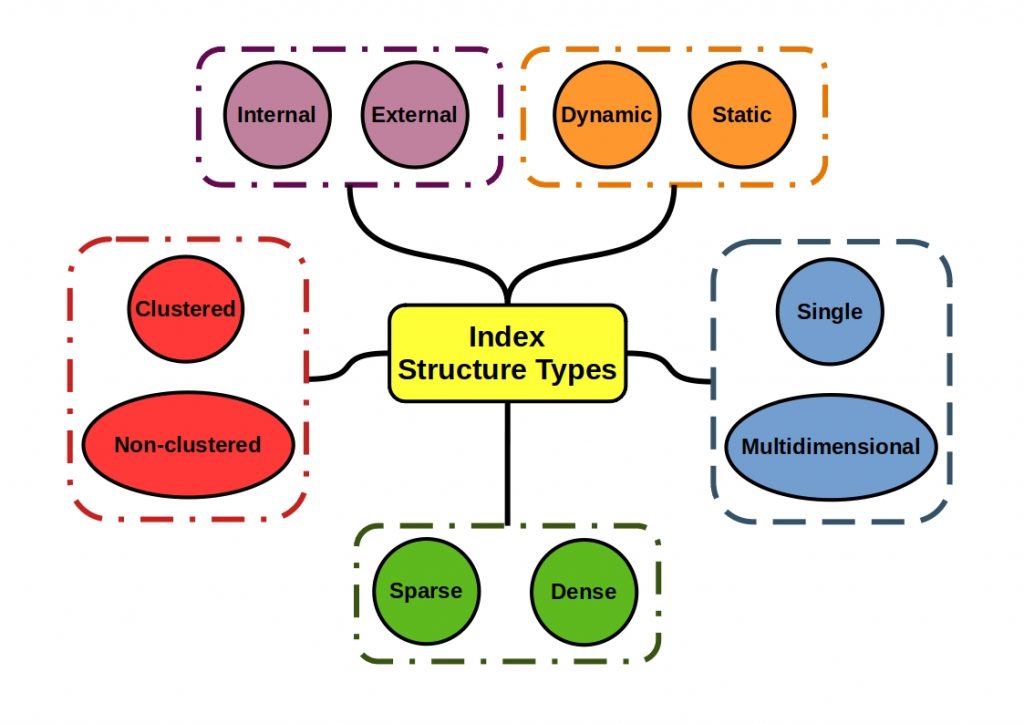
What are Messaging Patterns?

However, this form of message transmission is only one way of transferring information. The following figure shows the basic concepts of messaging design patterns.

This diagram shows all the basic components of the messaging design patterns — Basic Components of the Messaging Patterns

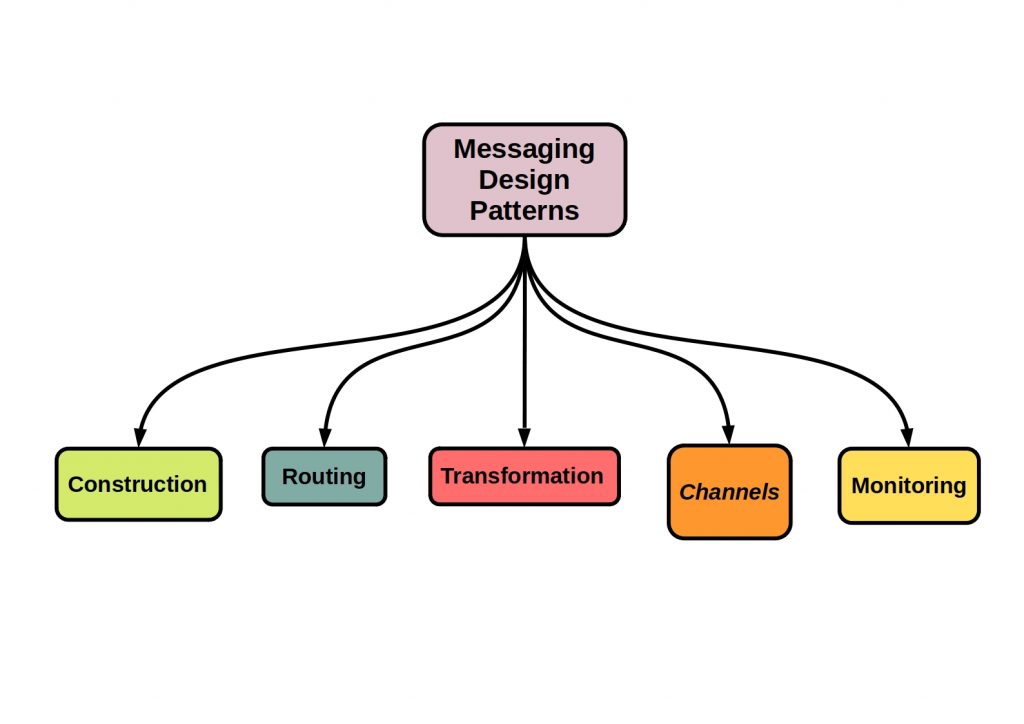
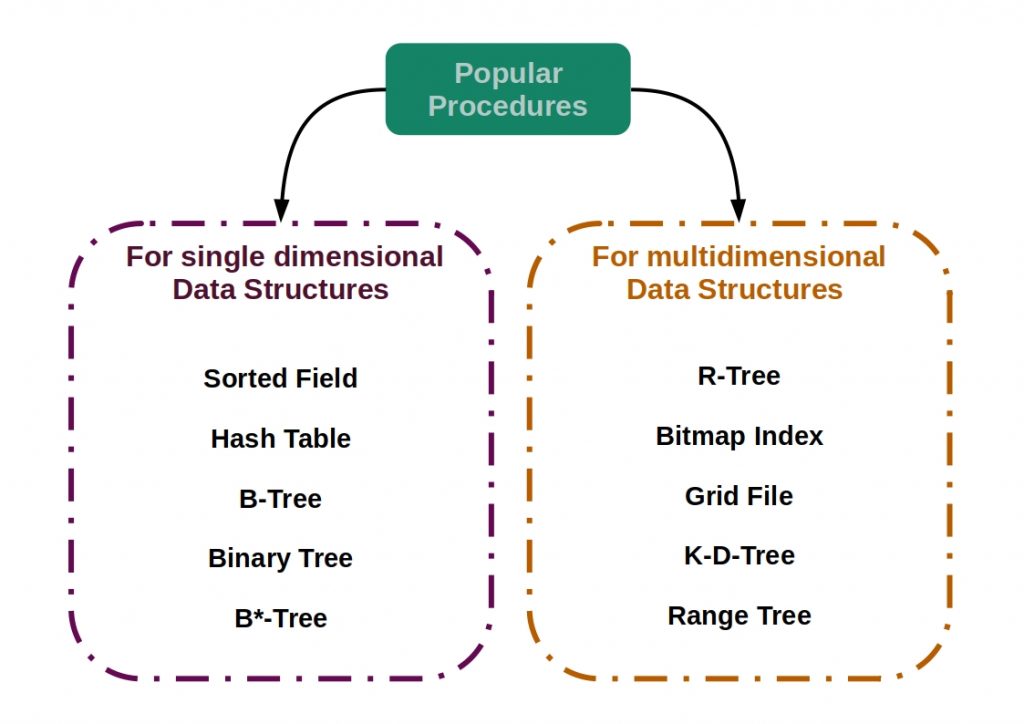
What is Message Construction?

It is not enough to decide to use a message. A message can be constructed according to different architectural patterns, depending on the functions to be performed.

The following figure shows some of these patterns.

Messaging Design Patterns - This diagram shows the different Patterns of message construction. — Messaging Design Patterns – Message Construction Patterns

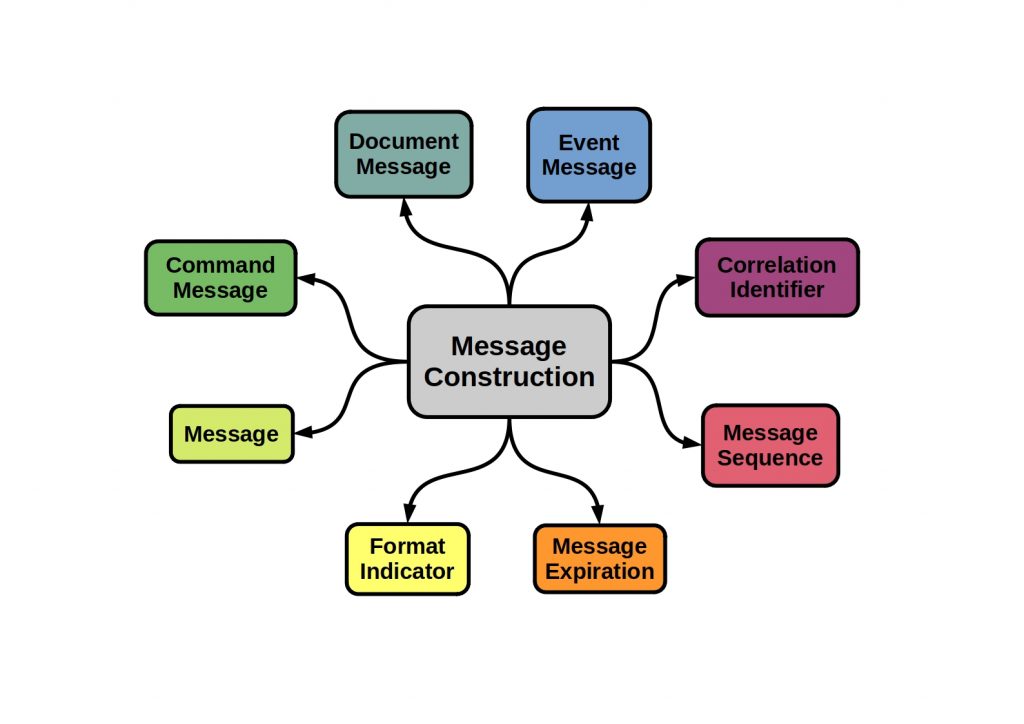
Message Construction – When do I use it?

Massaging can be used not only to send data between a sender and receiver, but also to call a procedure or request a response in another application.

With the right message architecture a certain flexibility can be guaranteed. This makes the message much more robust against possible future changes.

What is Message Routing?

A message router connects the message channels in a messaging system. We will come back to this topic later. This router corresponds to a filter, which regulates the message forwarding, but does not change the message. A message is only forwarded to another channel if all predefined conditions are met.

The following figure lists some specific message router types.

Messaging Design Patterns - This diagram shows the different patterns of message routing. — Messaging Patterns – Message Routing Patterns

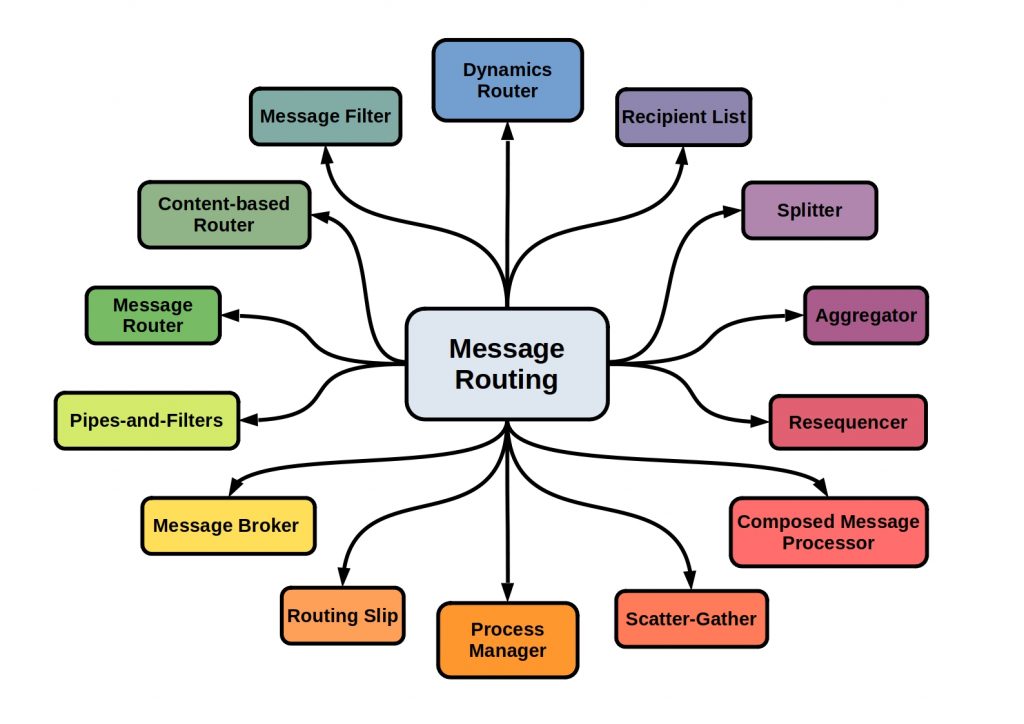
When do I use message routing and how?

For example, messages can be forwarded to dynamically defined recipients, or message parts can be processed or combined in a differentiated manner.

What are Messaging Channels?

In a messaging system, the exchange of information does not just happen unregulated. The sender transfers the message to a so-called messaging channel and the receiver requests a specific message channel.
In this way, the sender and receiver are decoupled. However, the sender can determine which application receives the data without knowing about it by selecting the specific messaging channel.

However, the right choice of message channel depends on your architecture. Which channel should be addressed and when?

The following figure lists some such channel types.

Messaging Design Patterns - This diagram shows the different patterns of message channels. — Messaging Patterns – Message Channel Patterns

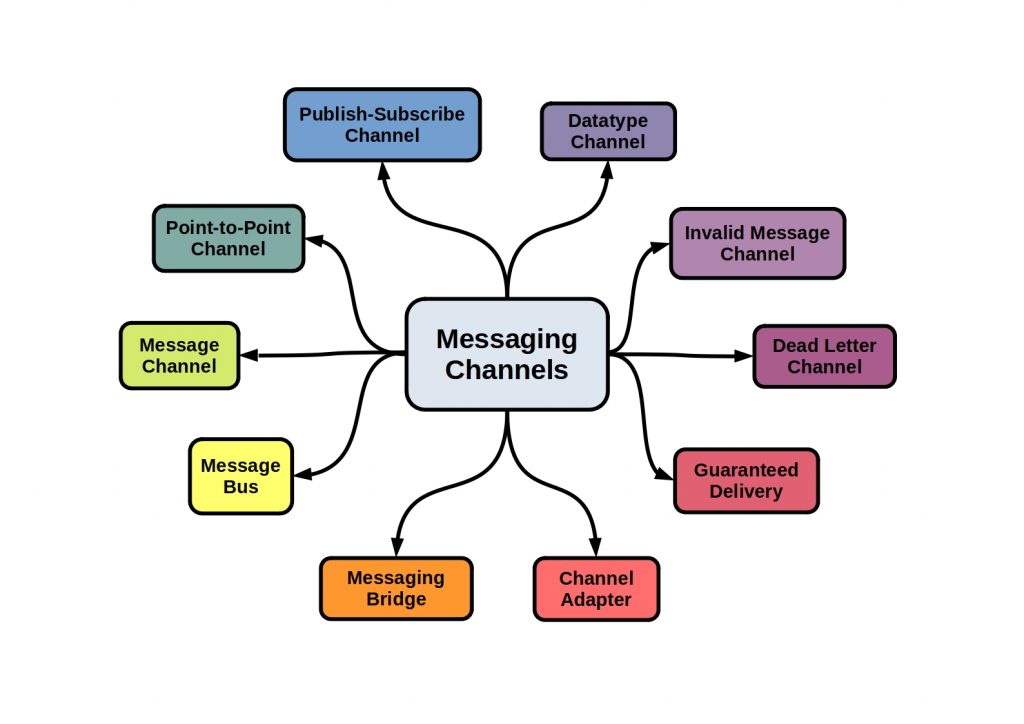
What are the basic differences between the channel types ?

Basically, the channel types can be divided into two main types.

A distinction can be made between a point-to-point channel, i.e. one sender and exactly one receiver, and a publish-subscribe channel, one sender and several receivers.

What is a Messaging Endpoint?

In order for a sender or receiver application to connect to the messaging channel, an intermediary must be used. This client is called a messaging endpoint.

The following figure shows the principle of communication via messaging endpoints.

Messaging Design Patterns - Dieses Diagramm zeigt the Basic principle of a message endpoint — Basic principle of a Message Endpoint

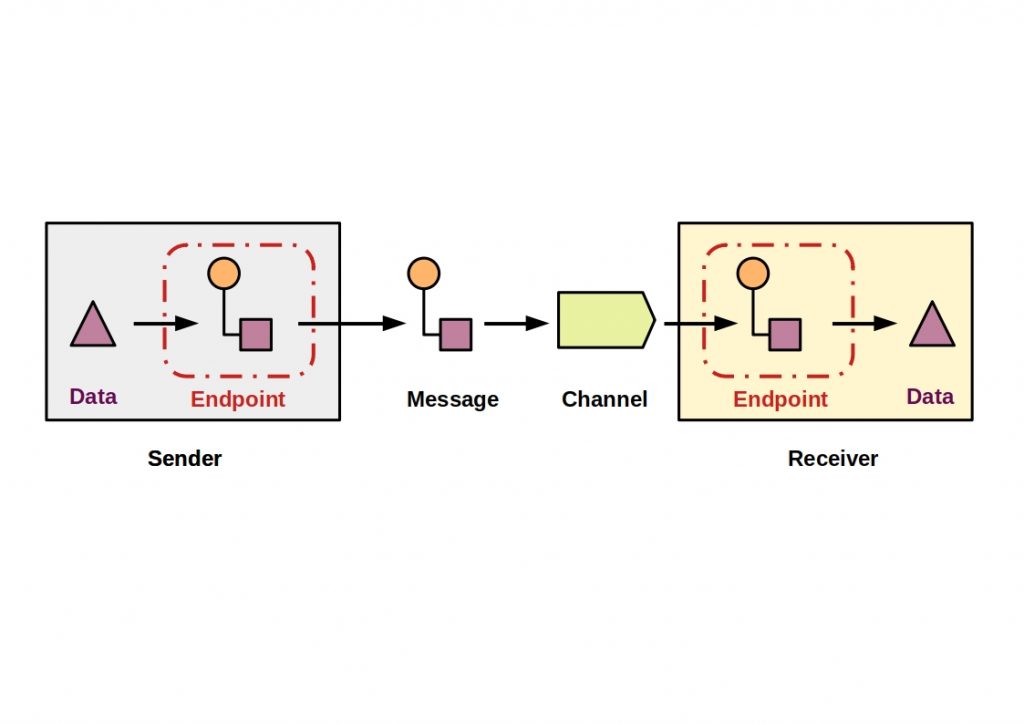
On the receiver side, the end point accepts the data to be sent, builds a message from it and sends it via a specific message channel. On the receiver side, this message is also received via an end point and extracted again. An application can access several end points here. However, an endpoint can only implement one alternative.

The following figure lists some endpoint types.

Messaging Design Patterns - This diagram shows the different patterns of message endpoints. — Messaging Design Patterns – Message Endpoint Patterns

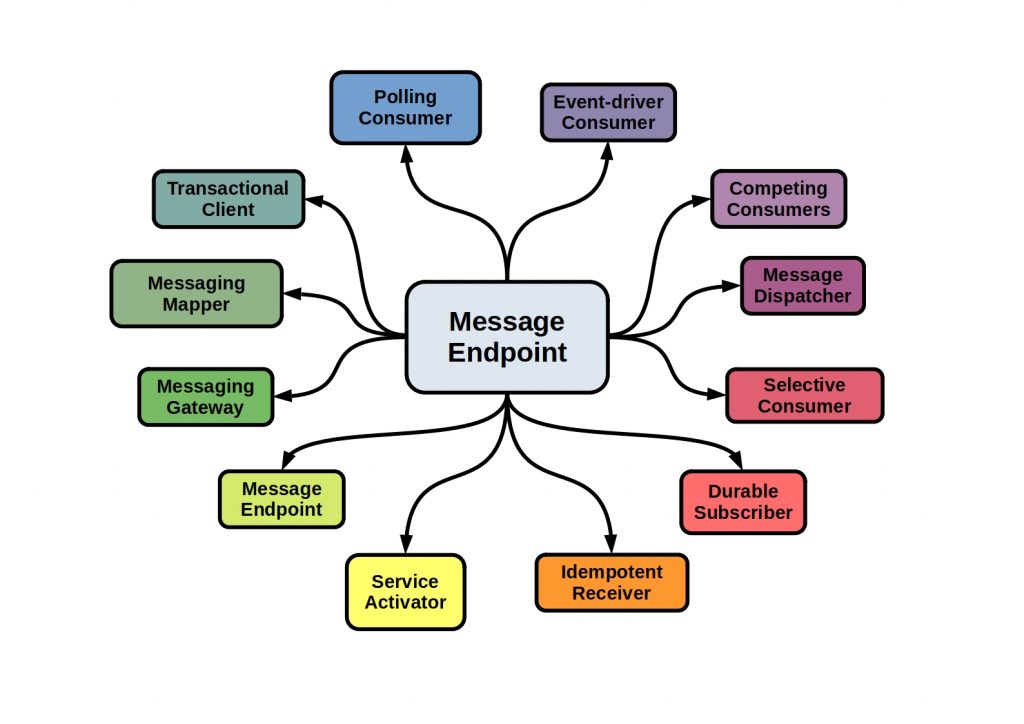
When do I choose which endpoint?

Receiving messages in particular can become difficult and lead to server overload. Therefore, control and possible throttling of the processing of client requests is crucial. A proven means is, for example, the formation of processing queues or a dynamic adjustment of consumers, depending on the volume of requests.

What is Message Transformation?

If the data format has to be changed when data is exchanged between two applications, a so-called message transformation ensures that the message channel is formally decoupled.

This translation process can be understood as two systems running in parallel. The actual message data is separated from the metadata.

The following figure shows some message transformation types.

Messaging Design Patterns - This diagram shows the different patterns of message transformation. — Messaging Design Patterns – Message Transformation Patterns

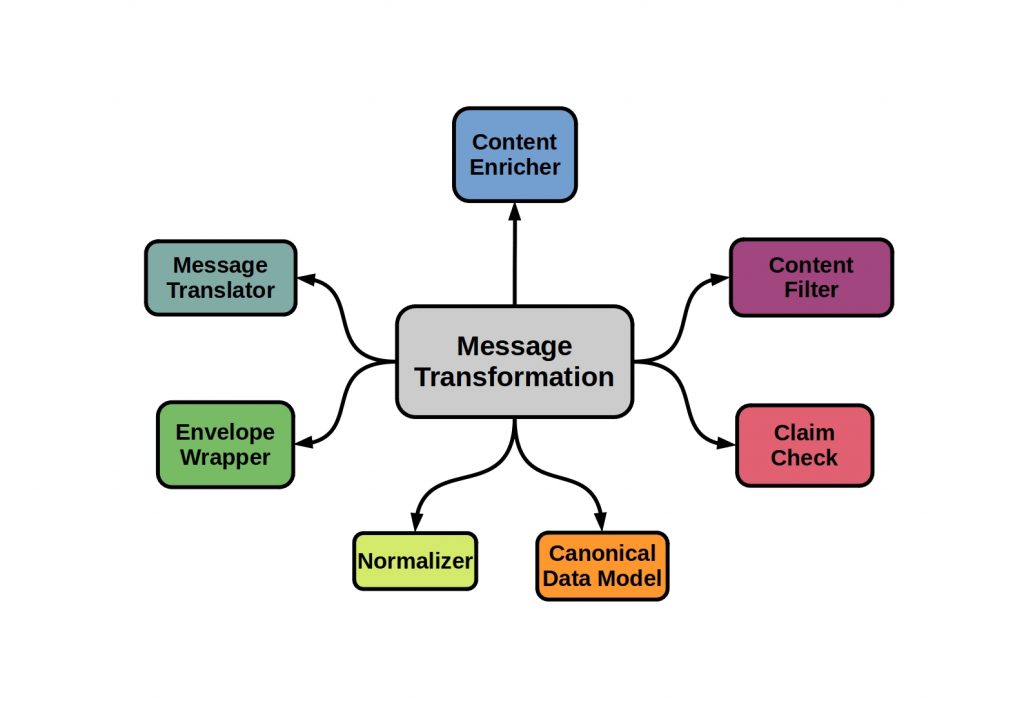
How do I monitor my messaging system and keep it running?

A flexible messaging architecture unfortunately leads to a certain degree of complexity on the other side. Especially when it comes to integrating many message producers and consumers decoupled from each other in a messaging system, with partly asynchronous messaging, monitoring during operation can become difficult.

For this purpose, system management patterns have been developed to provide the right monitoring tools. The main goal is to prevent bottlenecks and hardware overloads in order to guarantee the smooth flow of messages.

The following figure shows some test and monitoring patterns.

Messaging Design Patterns - This diagram shows the different patterns of message monitoring. — Messaging Design Patterns – Message Monitoring Patterns

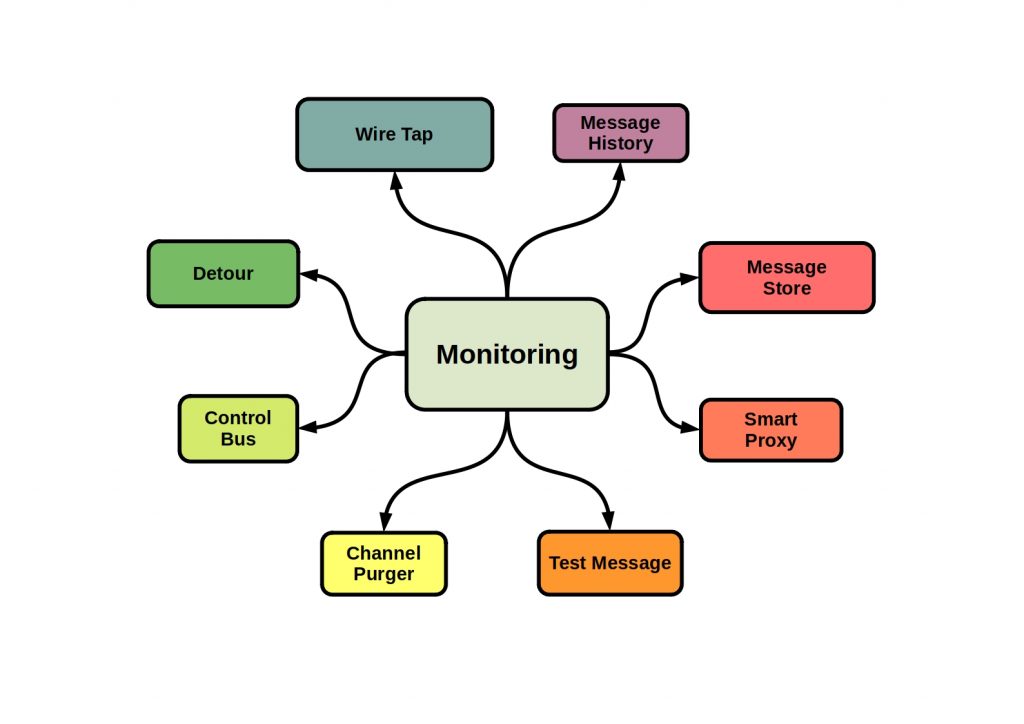
What are the basic systems?

With a typical system management solution, for example, the data flow can be controlled by checking the number of data sent and received, or the processing time.

This is contrasted with the actual checking of the message information contained.

jelleke vanooteghem RnBNnM2Utic unsplash

PCA vs Linear Regression – Therefore you should know the differences

January 16, 2021 / RainerGewalt / 2 Comments

PCA vs Linear Regression – Two statistical methods that run very similarly. However, they differ in one important respect. What the two methods actually are and what this difference is, we explain to you in the following article.

What is a PCA?

Principal Component Analysis (PCA) is a multivariate statistical method for structuring or simplifying a large data set. The main goal here is the discovery of relationships in 2 or 3 dimensional domain.
This method enjoys great popularity in almost all scientific disciplines and is mostly used when variables are highly correlated.

However, PCA is only a reliable method if the data are at least interval scaled and approximately normally distributed.
Although the variables are adjusted to avoid redundant effects, the error and residual variance of the data are not taken into account.

The following figure shows the basic principle of a PCA. High dimensional data relationships should be represented in a low dimensional way, with as little loss of information as possible.

PCA vs Linear Regression - Figure shows the basic principle of a PCA. High dimensional data relationships should be represented in a low dimensional way, with as little loss of information as possible. — PCA vs Linear Regression – Basic principle of a PCA

The key point of PCA is dimensional reduction. It is to extract the most important features of a data set by reducing the total number of measured variables with a large proportion of the variance of all variables.
This reduction is done mathematically using linear combinations.

What are linear combinations?

PCA works in a purely exploratory way, searching the data for a linear pattern that best describes the data set.
These linear combinations can best be thought of as straight lines between variable values.
In the figure below, the linear combinations have been applied to a data set.

PCA vs Linear Regression -In this scheme the linear combinations have been applied to a data set — Linear combinations

How does the algorithm work?

In the principal component analysis procedure, a set of fully uncorrelated principal components are first generated.
These contain the main changes in the data and are also known as latent variables, factors or eigenvectors.
The number of extracted components is given here by the data.

The first principal component is formed by minimizing the sum of squared variances of all variables.
During extraction, the variance component is maximized over all variables.
Then, the remaining variance is gradually resolved by the second component until the total variance of all data is explained by the principal components.

The first factor always points in the direction of the maximum variance in the data.
The second factor must be perpendicular to it and explain the next largest variance

PCA vs Linear Regression – How do they Differ?

We have studied the PCA and how it works in great detail. But what are the differences to linear regression?

In the following illustration the main difference is set up against each other.

PCA vs Linear Regression - The figure shows the main difference between the two methods. The minimization of the error squares to the straight line. — PCA vs Linear Regression – Minimization of the Error Squares to the Straight Line

With PCA, the error squares are minimized perpendicular to the straight line, so it is an orthogonal regression. In linear regression, the error squares are minimized in the y-direction.

Thus, linear regression is more about finding a straight line that best fits the data, depending on the internal data relationships.
Principal component analysis uses an orthogonal transformation to form the principal components, or linear combinations of the variables.

So this difference between the two techniques only becomes apparent when the data are not completely independent, but there is a correlation.

If you want to know more about machine learning methods and how they work, check out our article on the t-SNE algorithm.

t-SNE – Great Machine Learning Algorithm for Visualization of High-Dimensional Datasets

January 14, 2021 / RainerGewalt / 0 Comments

The machine learning algorithm t-Distributed Stochastic Neighborhood Embedding, also abbreviated as t-SNE, can be used to visualize high-dimensional datasets. Each high-dimensional information of a
data point is reduced to a low-dimensional representation. However, the information about existing neighborhoods should be preserved.

So this technique is another tool you can use to create meaningful groups in unordered data collections based on the unifying data properties. If you don’t know what cluster algorithms are, check out this article. Here we present 5 machine learning methods that you should know.
As shown in the following figure, the data should be represented grouped in 2-dimensional space.

The figure shows the data clusters generated by t-Distributed Stochastic Neighborhood Embedding (T-SNE) in 2-dimensional space. — Data clusters generated by t-Distributed Stochastic Neighborhood Embedding (T-SNE)

But how does the algorithm work and what are its strengths? In order to understand its function, we need to look at the origin of the technology.

What is the Stochastic Neighbor Embedding (SNE) Algorithm?

The basis of the t-Distributed Stochastic Neighborhood Embedding algorithm is originally the Stochastic Neighbor Embedding (SNE) algorithm. This converts high-dimensional Euclidean distances into similarity probabilities between individual data points.
The probability with which an object occurs next to a potential neighbor must be calculated.
The dissimilarities between two high-dimensional data points can be explained with a distance matrix, corresponding to the squared Euclidean distance.
A conditional probability is calculated for the low-dimensional correspondence.
This determines the similarity of the two data points on the low-dimensional map.

In order to achieve the closest possible correspondence between the two distributions pij and
qij, a Kullback-Leibler divergence (KL) over all neighbors of each data point is computed as a cost function C. Large costs are incurred for distant data points.

t-Distributed Stochastic Neighborhood Embedding: minimized cost function: sum of the Kullback-Leibler divergences between the original and the induced distribution over the neighbors of an object. — Minimized Cost function: sum of the Kullback-Leibler divergences between the original and the induced distribution over the neighbors of an object.

A gradient descent method is used to optimize the cost function. However, this optimization method converges very slowly. In addition, a so-called crowding problem arises.

If a high dimensional data set is linearly approximated in a small scale, then it cannot be reduced to a lower dimension with a local scaling algo-
rithm to a lower dimension.

What makes the t-Distributed Stochastic Neighborhood Embedding (t-SNE) Algorithmt work?

The t-Distributed Stochastic Neighbor
Embedding (t-SNE) algorithm starts here. On the one hand, a simplified symmetric cost function is used.

The figure shows the simplified symmetric cost function used in t-Distributed Stochastic Neighborhood Embedding. — t-SNE: simplified symmetric cost function

Here, only one KL is minimized over a common probability distribution of all
high, and low dimensional data is minimized.

On the other hand, the similarity of the low-dimensional data points is computed with a Student’s t-distribution and a degree of freedom of one. This can be optimized quickly and is stable to the crowding problem.
stable against the crowding problem.

Software Design Patterns – A COMPLETE GUIDE

January 13, 2021 / RainerGewalt / 1 Comment

Software Design Patterns – This article is intended to explain the concept of design patterns in a simplified way and to give you an overview of the individual major groups.

Software architecture can be compared to the architecture of a house. So needs the application development in the planning also consists of the design and the construction of a meaningful, stable structure.

During implementation, it is really only about problem definition and solution with the tools given to you. Many of the steps are repetitive and follow routine patterns. The experience of the user or architect plays a major role here.
What do I apply when and how?

What are Software Design Patterns?

For many processes, there are already very optimized, proven templates that can be reused. Through these so-called design patterns, it is therefore possible to indirectly access the experience of others. The concept goes back to the architect Christopher Alexander and was subsequently used by computer scientists as a basis for conceptual design in software architecture.

These Patterns are categorized on the basis their characteristics in so-called Design Pattern Catalogs and logically grouped around a certain clarity to create. These characteristics can be for example pattern similarities among themselves, the applicability, or the consequences. Many literature deal with this classification topic. The categorizations shown in the following figure may therefore differ depending on the point of view.

This diagram shows the 4 Important software design patterns. — 4 Important Software Design Patterns.

Creational Patterns

The Creational Design Patterns deal with object and class creation. How can object creations be inherited from other objects and to what extent can classes be instantiated by subclasses? How are these instantiations created and linked?

Patterns should create object creation mechanisms with which object creations are controlled and thus the object is created purposefully on the respective situation. Flexibility and reusability are the intended goals here.
Thereby the construction is separated from the concrete implementation.
In the following scheme some patterns, which are to be assigned to the creational patterns, are represented.

Software Design Patterns - This scheme shows some Creational Patterns examples — Software Design Patterns **– Creational Patterns examples**

Structural Design Patterns

How do I create large, cohesive, yet efficient structures? How do I properly optimize the interaction of my entities? Structural Design Patterns should help with these questions and standardize the composition of objects and classes. So the focus here is on establishing individual relationships.
The following figure shows some of the patterns assigned here.

Software Design Patterns - This scheme shows some Structural Patterns examples — Software Design Patterns **-Structural Patterns examples**

It is often a matter of optimizing and saving inheritance processes. For example, objects can be enclosed in a tree structure, which then all use the same interface, or general properties can be moved to a single object, which is then shared by all other objects. Pipelines can be built and process chains can be formed.

Behavioral Patterns

In addition to the efficient assignment and allocation of entities, communication must also be optimized. At this level, the different transfers among them also describe a structural flow of control. These behavioral patterns can be very complex and difficult to grasp, but are determined by how the individual objects are connected to each other.

So how are responsibilities distributed? Behavioral patterns are intended to help increase the flexibility of the software in terms of its behavior in carrying out this communication.
In the following diagram some patterns are represented, which are to be assigned to the Behavioral Patterns.

Software Design Patterns - This scheme shows some Behavioral Patterns examples — Software Design Patterns – **Behavioral Patterns examples**

For example, inheritance between classes is used to distribute behavior between classes. This inheritance is a sequence of different algorithms that retrieve operations in predefined order and are defined, instantiated, and implemented.
Also, behaviors of objects can be encapsulated instead of distributing them across classes. Another behavioral pattern approach is an observer pattern where the dependencies between objects are observed.

Concurrency Patterns

Like also computations at the same time, thus parallel can be executed, so also models can be created parallel.
So whole program instances can be encapsulated as processes and run isolated, or a program can be divided into several threads, which all access the same memory area, but can also work in parallel.
Where which pattern can be used depends on all the workload conditions present and must be carefully coordinated to effectively avoid overload peaks. The following diagram shows some examples of concurrency patterns.

Conclusion

Since not every problem solution has to be developed by oneself, strategically applied design patterns can save time and resources. They can ensure that programs run effectively. A certain standardization is created. This is especially important for cross-team development. A software product is thereby uniformly and coherently conceived and implemented.

Nevertheless, these templates are often criticized. Why is that?
A decisive factor is that design patterns must not be seen as an all-purpose solution. The individual templates must be understood by the developer in order to use them efficiently. Does the template fit my problem 100 percent, or am I creating extra work again?

Design patterns allow you to access the experience of others, but require your own experience in working with these solutions.

If you are interested in more architectural thinking. Here we have put together another interesting software design the Domain Driven Design.

AI vs Machine Learning vs Deep Learning – It’s almost harder to understand all the acronyms around AI than the technology itself.

January 5, 2021 / RainerGewalt / 5 Comments

It’s almost harder to understand all the acronyms around Artificial Intelligence (AI) than the technology itself.
AI vs Machine Learning vs Deep Learning – These terms are often carelessly mixed together. But what are actually the differences? In this article, we will introduce you to all Three fields, because even though there is overlap, they differ.
It should be important for you to know these differences, as each discipline describes different stages of a data analysis pipeline.

AI vs Machine Learning vs Deep Learning

In the following figure, we have schematically shown you the individual fields in their context. As you can see, the individual disciplines surround each other and form an onion-like layered model.

The figure clearly shows that there are relationships between individual disciplines. AI is to be understood as a generic term and thus includes the other fields. The deeper you go in the model, the more specific the tasks become. In the following, we will follow this representation and work our way from the outside to the inside.

Artificial intelligence

All disciplines are encompassed by the term AI. It is a science that explores ways to build intelligent programs and machines that can perceive, reason, act, and solve problems creatively. To this end, it attempts to model how the human brain works.
The following figure shows that AI can basically be divided into two categories.

Classification is about measuring the performance of AI based on how well it is able to replicate the human-like brain. In the Based on Functionality category, AI is classified based on how well it matches the human way of thinking. In the second category, it is evaluated based on human intelligence. Within these categories, there are still some subgroups that correspond to an index.

AI vs Machine Learning

So what is the first subcategory Machine Learning and how does it differ from AI?
While AI deals with the functioning of artificial intelligence and compares them with the functioning of the human brain, machine learning is a collection of mathematical methods of pattern recognition. It is about how a system is given the ability to automatically learn and improve from experience. Various algorithms (e.g., neural networks) are used for this purpose. In the following scheme, the broad machine learning field is presented in a categorized way.

In machine learning, algorithms are used to build statistical models based on training data. Roughly, these algorithms can be divided into three main learning techniques. While in supervised learning the result is predetermined by a cleanly labeled data set, unsupervised learning is completely self-organized. Here the patterns are to be explored independently.
In reinforcement learning, utility functions are to be independently approximated based on rewards received.

Machine Learning vs Deep Learning/ Deep Neural Learning

Deep learning is a subfield of machine learning similar to machine learning in Ai. Here, multilayer neural networks are used to analyze various factors in large amounts of data. These networks are similar to the human neural system. If you want to know more about this structure, read our article on perceptrons, the smallest unit of a neural network.
Optimization of neural weights, unlike machine learning, can be done using powerful GPUs. Pure machine learning is best used on structured data sets, while for unstructured data you should opt for deep learning. In the following graphic, we have summarized the main factors that make up deep learning. For the network types autoencoder and CNN we provide more detailed articles.

Representation of all basic deep learning components
AI vs Machine Learning vs Deep Learning — Definition Deep Learning

4 Index Data Structures a Data Engineer Must Know

January 2, 2021 / RainerGewalt / 1 Comment

In this article we will explain what index data structures are and introduce you to some popular structures.

In today’s world, ever-increasing amounts of data are being processed. The data can be used to derive business strategies in a commercial context, but also to gain valuable information about all scientific disciplines. The data obtained must be saved, ideally as raw data, and stored for future analysis.

At the time of creation, it is not yet possible to estimate what information might be valuable at some point. So any reduction in data ultimately represents a loss. Huge amounts of data accumulate every second, and managing them is an immense task for today’s hardware and software. Mathematical tricks have to be used to optimize search mechanisms and storage functions.

Index data structures allow you to access searched data in a large data collection immensely faster. Instead of executing a search query sequentially, a so-called index data structure is used to search for a specific data record in this data set based on a search criterion.

What are Index Data Structures in Databases?

You have probably heard about indexing in connection with databases. Here, too, an index structure is formed, independent of the data structure, which accelerates the search for certain fields. This structure consists of references, which define an order relation to the table columns. Based on these pointers, the database management system can then find the data using a search algorithm.

schematic representation of index data structures in databases — Index Data Structures in databases

However, indexing is a very complex scientific field. Queries are constantly being made more efficient and optimized. Thus, the approaches are diverse and very mathematical. This article will give you an overview of popular index data structures and help you to optimize your data pipelines.

Index data structure types

There are many different indexing methods. They are all based on different mathematical assumptions. You should understand these assumptions and choose a suitable system according to your data properties.
In the following scheme you can see some structure types you have to distinguish between, depending on the data you want to index.

index structures 1 — index data structure types

The most important distinction, however, is whether you want to index one-dimensional or multidimensional data relationships. This means that you have to differentiate whether there is a common feature or several related but independent features.
In the following figure, we have classified the individual index structures according to their dimension coverage.

we have classified the individual index structures according to their dimension coverage. — individual index structures according to their dimension coverage

Which index structure you ultimately choose depends on many factors and should be weighed up well in advance, especially with large data sets.

Popular index data structures you should know

In the following, we will introduce you to some of the most popular indexing methods in detail. Because here, too, the key to success lies in understanding your tools and using them correctly at the right moment.

What is Hashing?

If you want to search for a value in an unsorted array, a linear search method is not optimal and too time consuming.
With the so called hashing method a hash value is used for unique object identification. This is calculated by a hash function from the key and determines the storage location in an array of indices, the so-called hash table. This means that you use this function to generate a unique storage location in the table using a key.
In the following figure the hash function flow is shown again.

schematic representation of the hash function sequence in detail — hash function sequence

Important basic assumptions are, however, that the function always returns a number for an object, two identical objects always have the same number and two unequal objects do not always have different numbers.

What is a Binary tree?

A so-called binary tree is a data structure in which each element, also called node, has a maximum of two successors. The addresses of the subordinate nodes are kept track of by pointers. It is often used when data is to be stored in RAM.

What is a B-tree?

The B-tree is often used in databases and file systems, i.e. for storage on the hard disk. The tree is sorted and completely balanced. The data is stored sorted by keys. The keys are stored in its internal nodes, but need not be stored in the records at the leaves. CRUD functions run in amortized logarithmic time.

The B-tree is classified into different types according to its properties.
In the B+ tree, only copies of the keys are stored in the internal nodes. The keys are stored with the data in the leaves. To speed up sequential access, these also contain pointers to the next leaf node and are thus concatenated.
In the following scheme you see a basic B+ tree structure.

Basic representation of a b+ tree and its components — Basic b+ tree structure

The B* tree is an index structure where non-root nodes must be at least 2/3 filled. This is achieved by a modified split strategy.
In addition to indexing, partitioning also offers you the possibility of strongly optimizing the data search within a database. In this article we introduce you to this technique.

What is a SkipList?

The SkipList resembles in its structure a linked list consisting of containers, which contain the data with a unique key and a pointer to the following container. In a SkipList, however, the containers have different heights and can contain pointers to containers that do not follow directly. The idea is to speed up the search by additional pointers.

schematic representation of an index structure of the SkipList — Schematic representation of a SkipList

Calculation of the container height

All nodes have pointers on different levels. Keys can be skipped with it. The height of the list elements is calculated either regularly, or unbalanced according to mathematical rules. The search is however dependent on the list emergence or evenly randomly over the list.

When to choose NoSQL over SQL?

December 29, 2020 / RainerGewalt / 1 Comment

When to use NoSQL vs SQL – In this article we explain the important differences.
With the right choice of storage medium, you can build elementary more performant architectures in times of Big Data. Streaming platforms can now process huge streams of data in real time. But this technology is not a panacea. The database, for example, still occupies an important place in today’s data handling.
Often, however, it is crucial that you choose the right system for your data and in relation to the overall infrastructure.

when to use NoSQL vs SQL – Spoiled for choice

Database vendors abound. Here is just a small selection of popular databases.

popular examples nosql sql — Popular SQL and NoSQL Databases

But before you get into the differences between the databases, you should basically know the differences between the systems.

SQL is relational

Structured Query Language (SQL) databases consist of a fixed defined schema structure. All schemas contain tables with columns. Each table row (tuple) represents a data set (record). In addition, each row consists of a set of attributes (characteristics).

You can use the query language to manipulate and retrieve tables. You can also control the relationships between these structured data formats. Each table in a database can be linked to each other.
These relationships can take many forms. Table cells can have single relationships, or relationships with many cells.

This schema clearly shows all SQL table cells elationships — SQL table cells relationships

NoSQL is not relational

Not only SQL (NoSQL) databases allow you to store and retrieve unstructured data using a dynamic schema. For example, your data is stored in the form of n collections, each containing m documents. Other forms are key-value stores, or graph databases. Thus, there is no special query language here

when to use NoSQL vs SQL – Both in direct comparison.

NoSQL databases exist since 1998 and is relatively young compared to SQL. SQL was already developed in the 70s. Besides the actual structure, databases of both categories differ in that they are scalable in different ways. In contrast to
NoSQL databases, SQL databases can only be scaled vertically.
Furthermore, it is important for you to know that you cannot write to and read from an SQL database in parallel. In NoSQL databases, you can read what data is available at that moment.

When to use NoSQL vs SQL

Which one suits me?

As you might have guessed, the answer here is: it depends! The differences are there and can have an important impact on the performance of your services. So the choice always depends on the application purpose. Especially for BigData use cases you should choose a NoSQL database, because here you don’t have to wait for the transaction to complete. Where you need high flexibility, due to frequently changing data structures, or real-time processing, you should also go for NoSQL DBs. However, if you want acid guarantees, you will have to go for an SQL solution. It is important for you to understand that both systems coexist, complement each other and do not replace each other.

If you want to know how to partition a database, check out this article.

H2O AI – That’s why it’s so great

December 5, 2020 / RainerGewalt / 0 Comments

There is a lot of Big Data software available now. One of them that you should definitely know about is the H2O AI Machine Learning solution.

With this open-source application you can implement algorithms from the fields of statistics, data mining and machine learning. The H2O AI Engine is based on the distributed file system Hadoop and is therefore more performant than other analysis tools. Your machine learning methods can thus be used as
parallelized methods.

Software Stack

They can program their algorithms in R, Python and Java and thus in the most important mathematical programming languages. H2O provides a REST interface to Python, R, JSON and Excel. Additionally, you can access H2O directly with Hadoop and Apache Spark. This makes integration into your data science workflow much easier. You already get approximate results while running the algorithms. A graphical web browser UI helps you to better analyze the processes and perform targeted optimizations.

How Clients Interacts with H2O AI

You can interact with H2O via clients using various interfaces. It is important for you to know that the data is usually not held in memory. They are localized in a H2O cluster and you only get a pointer to the data when you make a request.

H2O Frame

The basic unit of data storage accessible to you is the H2O Frame. This corresponds to a two-dimensional, resizable and potentially heterogeneous data point. This tabular data structure also contains labeled axes.

H2O Cluster

Your H2O cluster consists of one or more nodes. A node corresponds to a JVM process and this process consists of three layers.

H2O Machine Learning Software Structure — H2O Software Stack

H2O Machine Learning Components

Language Layer

The R evaluation layer is a slave to the REST client front-end and in the Scala layer you can write native programs and algorithms. You can then use these with H2O Machine learning.

Algorithms Layer

This layer is where your algorithms are applied. You can run statistical methods, data import and machine learning here.

Core Layer

In this layer you handle the resource management. You can manage both the memory and the CPU processing capacity.

Microsoft Power Platform – To turn your company into an Industry 4.0 enterprise, you can no longer avoid cloud solutions

November 28, 2020 / RainerGewalt / 0 Comments

In this article, we will show you everything about the cloud-based web tool Microsoft Power Platform and why you shouldn’t do without it.

Cloud-based web development has gained popularity in the web development industry in recent years. The globalization of the workforce and the diversification of the work process have significantly driven the development of cloud-based services.

What is Microsoft Power Platform?

With Power Platform you get an integrated application platform consisting of a group of different Microsoft products with which you can develop complex business solutions. This way you can make your business processes more efficient and productive. The platform can also take care of data storage, entry and processing. Data analysis via complex visualizations and predictions can also be handled by various services.

Microsoft Power Platform Services

Since the Power Platform is a collection of different Microsoft services, we want to give you an overview of the individual parts.

Build your own Apps

With Power Apps you get a user suite for mapping custom apps. All apps are independent of data sources and can be extended by you as you wish via drag & drop. This way you can adapt them to your needs.

Automate your tasks

Power Automate was still called Microsoft Flow until 2019. This web tool lets you automate recurring tasks and simple cross-platform workflows. You can connect to over 100 third-party systems via connectors. This allows you to automate processes outside the Microsoft environment and across applications.

Schematic representation of the Principle Microsoft Power Automate — Principle Microsoft Power Automate

Analyze your business data

With Power BI you get a business intelligence tool. With this you can access different data sources. An advantage to other BI tools is the deep integration with Excel. So you can create user-friendly, data connections and visualize.

Should I choose Microsoft Power Platform?

You need more and more scalable and secure solutions at low cost. Device-independent access to important planning and evaluation software will increasingly become the focus of attention and change global corporate structures. To turn your company into an Industry 4.0 enterprise, you can no longer avoid cloud solutions.

The question is not: if, but when you will choose a corresponding service. The question is not: if, but when you will choose a corresponding service. Microsoft, as one of the largest IT companies, now presents you with a solution. Whether it fits your needs, however, you must ultimately decide for yourself.

Array vs Object – The creation of a JSON structure follows some rules you should know

November 26, 2020 / RainerGewalt / 3 Comments

Array vs Object – JSON is one of the most popular data formats. However, the creation of such an object is done according to some rules. These rules depend on the original data type. In this article we will introduce you to the conversion of some JSON data types (Array vs Object).

What is JSON anyway?

With the JavaScript Object Notation, JSON for short, you can structure data compactly and independently of programming languages. The data format is therefore particularly well suited for exchange between your applications, for general data storage (file extension “.json”) and for configuration files. The data is also readable for you and coded in the standardized text format. The application notes of the data format are defined by the standards – RFC 8259 and the JSON syntax by the standards ECMA-404. Due to its easy integration with JavaScript, you can use it well for transferring data in web applications.

You can best compare the JSON data structure to XML and YAML, only it’s simpler and more compact.

What are the basic rules?

This code snippet shows a simple json object structure — Simple JSON Object

The JSON text structure is based on the JavaScript Object Syntax. Hierarchical data structures are thus possible. It contains only properties and no methods. The basis is formed by name-value pairs and ordered list of values. Basically, they are formatted with curly braces and as strings. This is especially advantageous if you want to transfer the data over the network. If you want to access the data you have to convert the text structure into a native JavaScript object.

Data Formats – JSON Array vs Object

Basically, you can have different data types included in JSON.

Value:

Your JSON value can take one of the following allowed types.

Object:

A JSON object represents the basic form of a JSON text. With this you can accept any data type that is suitable for inclusion in JSON.

Array:

JSON Array vs Object – It is possible to include an array. Arrays can contain objects, strings, numbers, arrays and boolean. You can include arrays as shown schematically below, enclosed with two square brackets.

In this way, you can further and further nest the individual data types with each other and thus easily create any number of hierarchy levels. For example, object attributes can consist of arrays, or arrays can contain multiple objects.